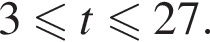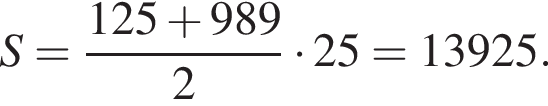30. Задание № 900 
Сложность: V
Числа и их свойства, сравнение чисел
i
Найдите сумму всех трехзначных чисел, которые при делении на 4 дают в остатке 1, при делении на 6 дают в остатке 5 и при делении на 9 дают в остатке 8.
Решение. Числа, которые делятся на 4 и дают в остатке 1: 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49..
Числа, которые делятся на 6 и дают в остатке 5: 11, 17, 23, 29, 35, 41, 47, 53..
Числа, которые делятся на 4 и дают в остатке 1 и делятся на 6 и дают в остатке 5: 17, 29, 41, 53, 62..
Числа, которые делятся на 9 и дают в остатке 8: 17, 26, 35, 44, 53...
Числа, которые делятся на 4, 6 и 9 с заданными остатками: 17, 53...
Тогда получаем 36t+17. Имеем:  при целых
при целых 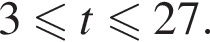
Получаем: 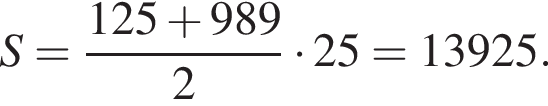
Ответ: 13925.
Ответ: 13925
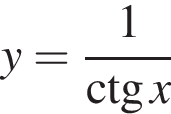 не определена в точке:
не определена в точке: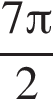
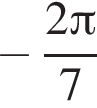
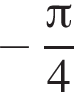
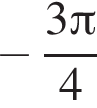
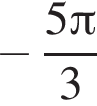
![]() не определена, когда
не определена, когда 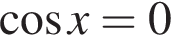 или когда
или когда 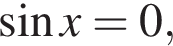 т. е. при
т. е. при 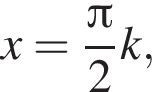 где
где ![]() Таким образом, она не определена в точке
Таким образом, она не определена в точке ![]()

 равна 360°, поэтому четвертый угол равен 140°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 40°.
равна 360°, поэтому четвертый угол равен 140°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 40°.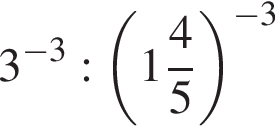 равно:
равно: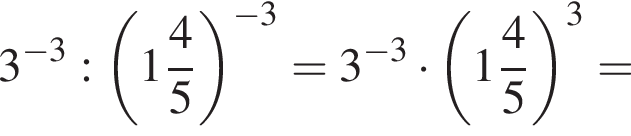
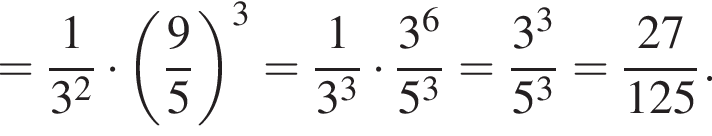
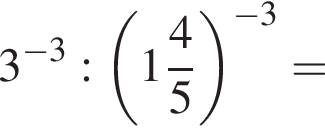
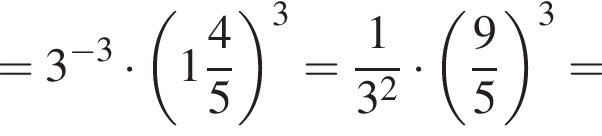
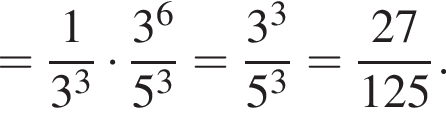
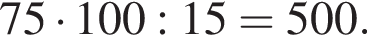 Таким образом, меньшее число
Таким образом, меньшее число 
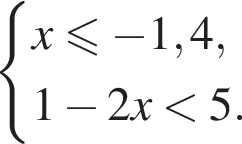
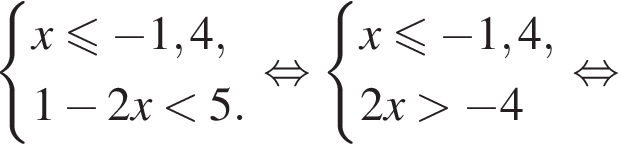
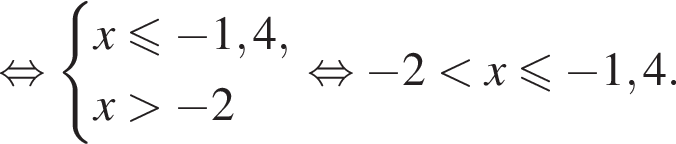
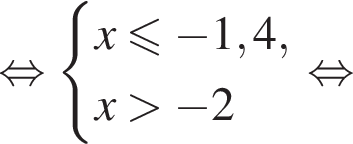
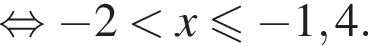
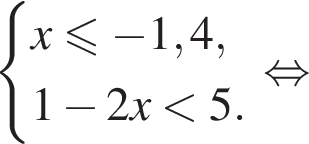
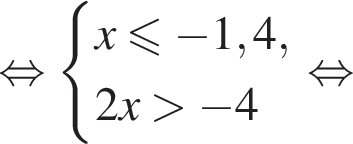
 Тогда:
Тогда: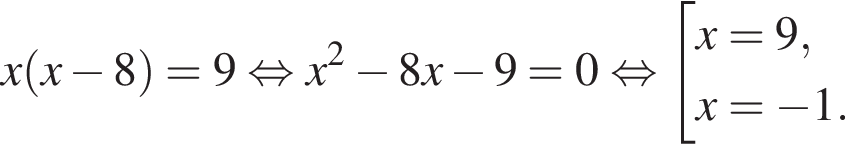
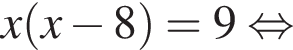
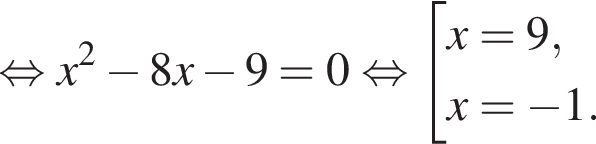
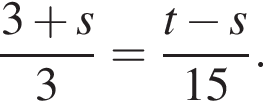
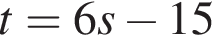



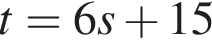
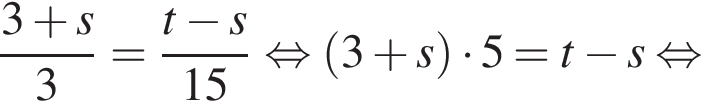
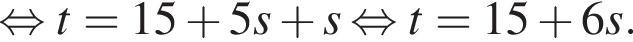
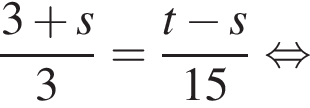
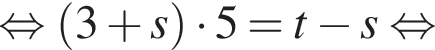

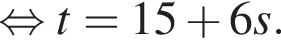
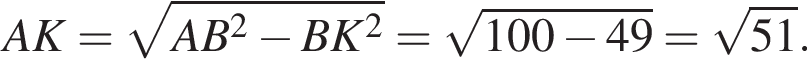
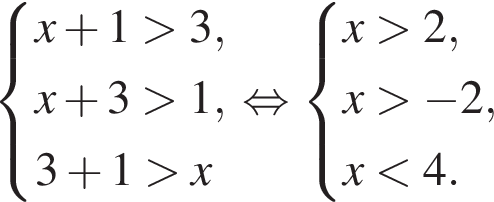
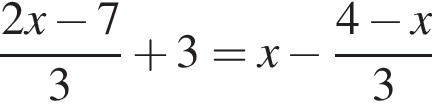 равносильно уравнению:
равносильно уравнению:

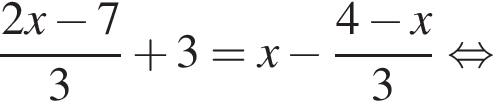
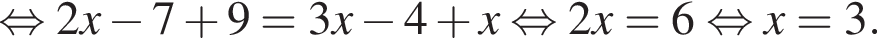

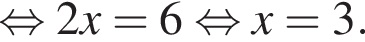
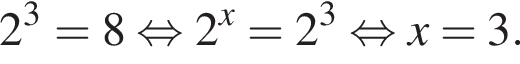
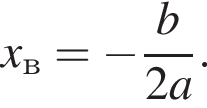 Поэтому
Поэтому 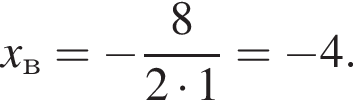 Поскольку y(xв) = −3, имеем:
Поскольку y(xв) = −3, имеем: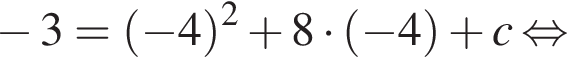

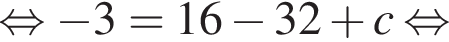
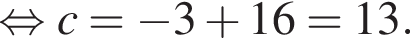
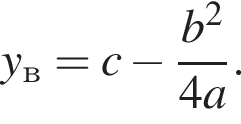
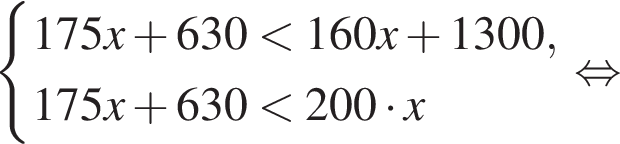
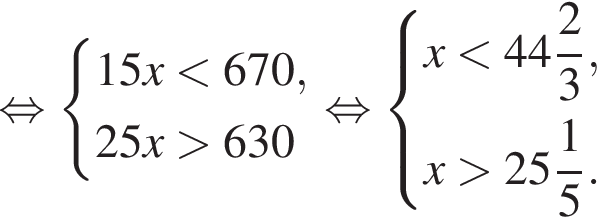
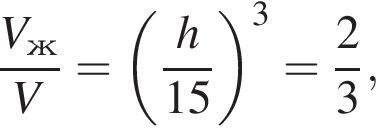 откуда
откуда 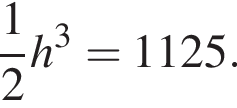
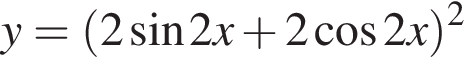
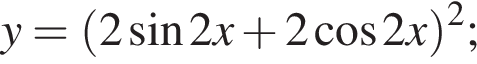
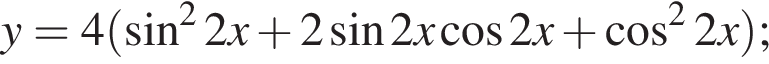

 имеем:
имеем:
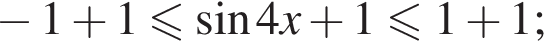
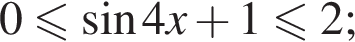
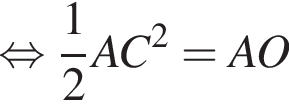

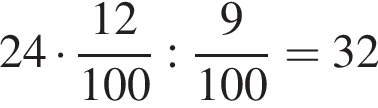 л.
л.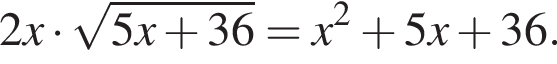
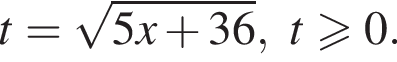 Тогда:
Тогда: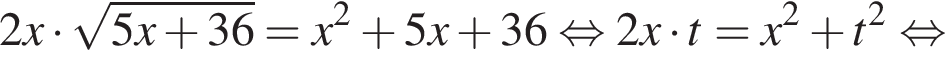

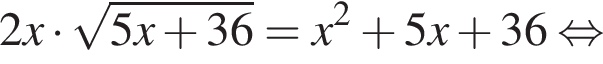


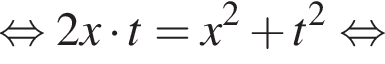
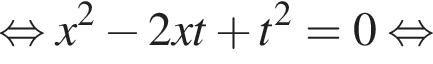
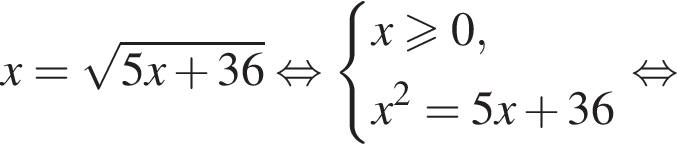
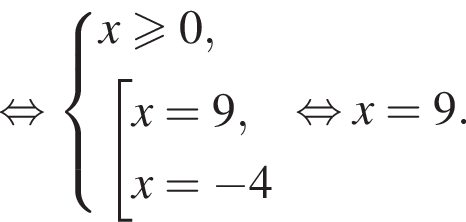
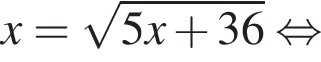
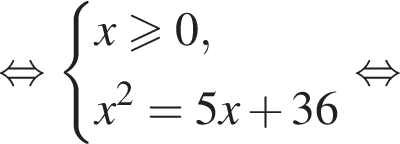

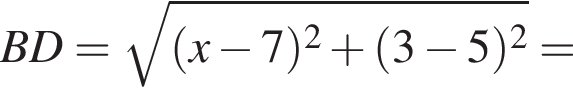
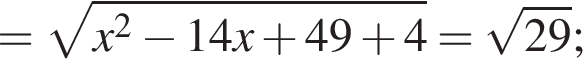
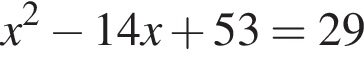
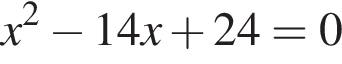
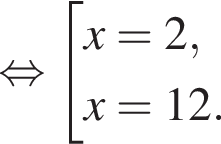
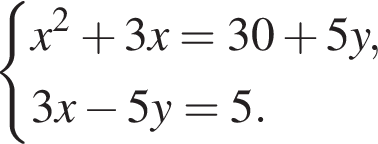
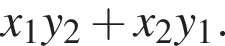
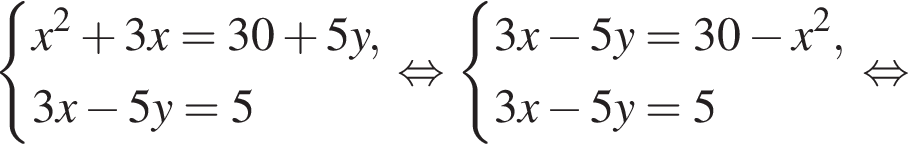
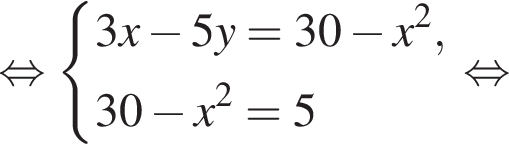
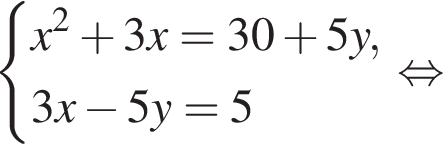
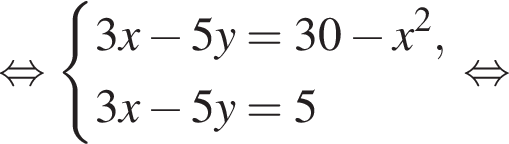
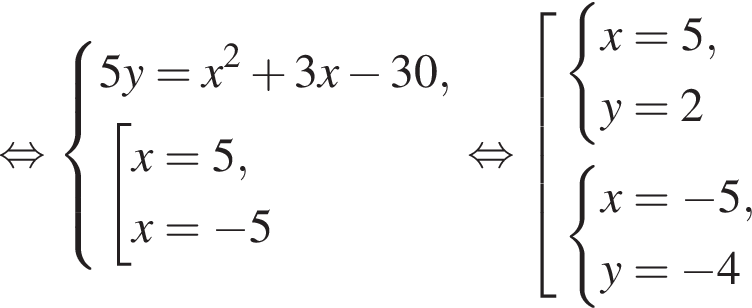

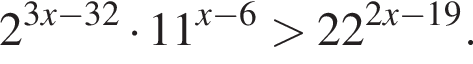
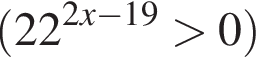 :
: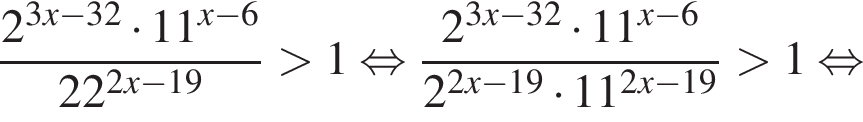
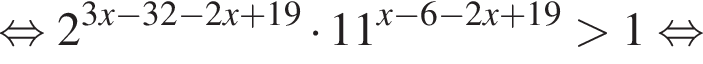
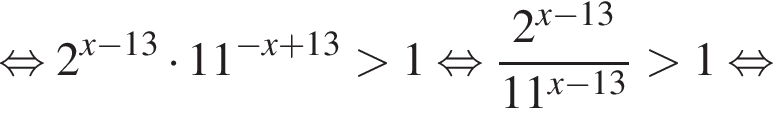
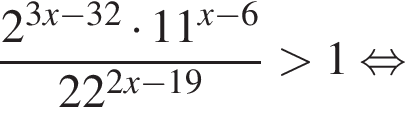
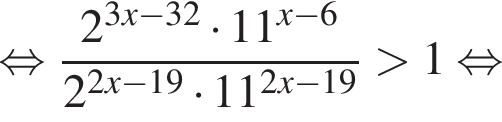
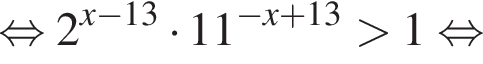
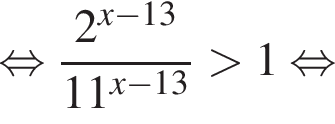
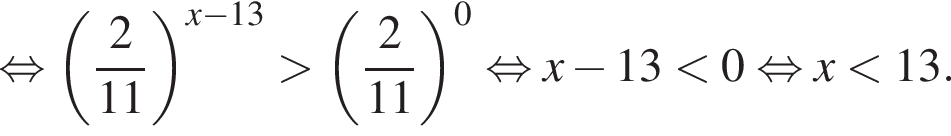
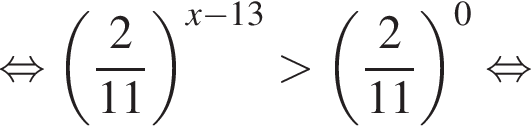
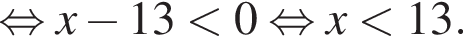
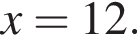
 на промежутке
на промежутке 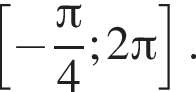

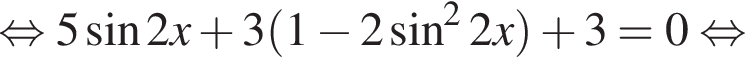
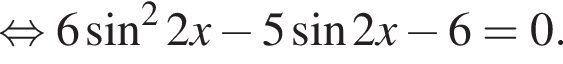
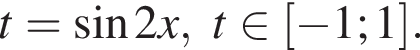 Тогда:
Тогда: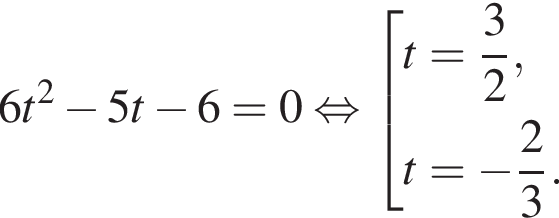
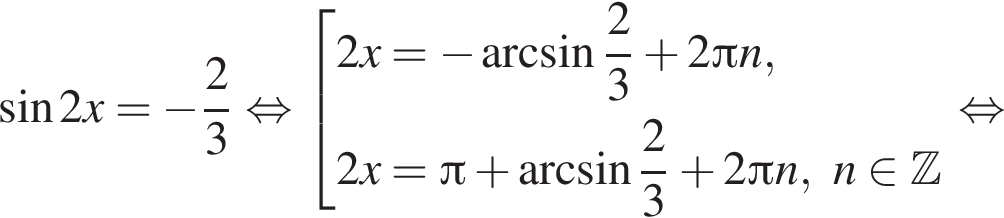
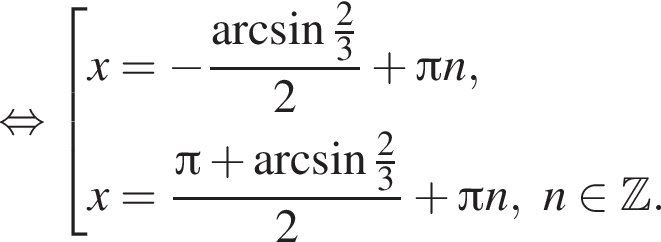
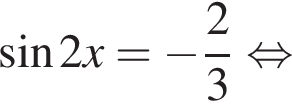
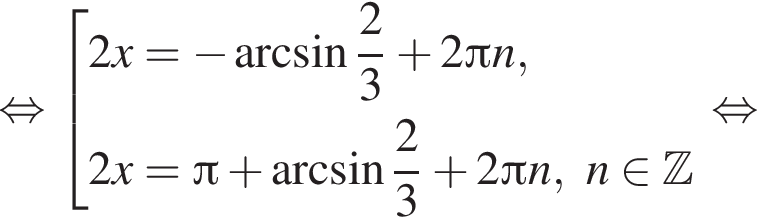
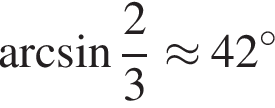 . Рассмотрим значения x при различных значениях n:
. Рассмотрим значения x при различных значениях n: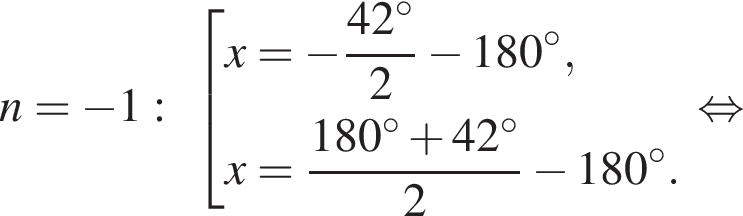
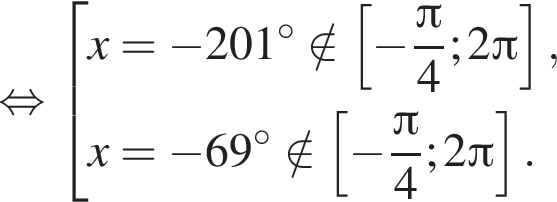
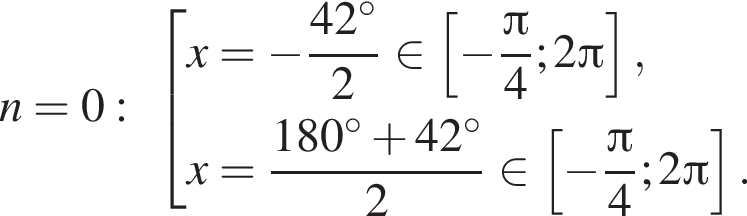
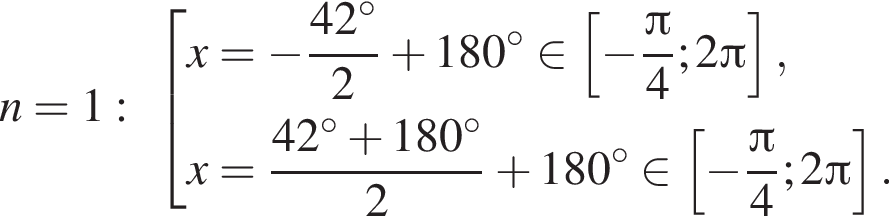
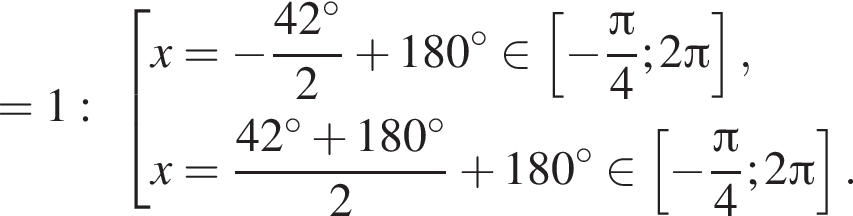
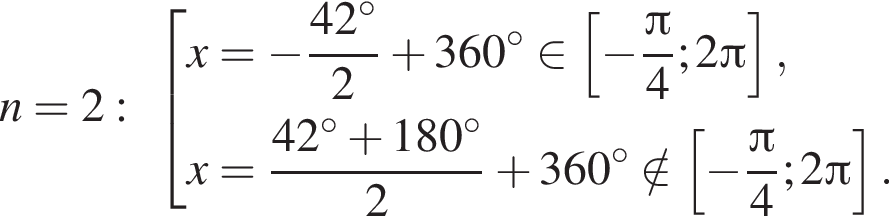
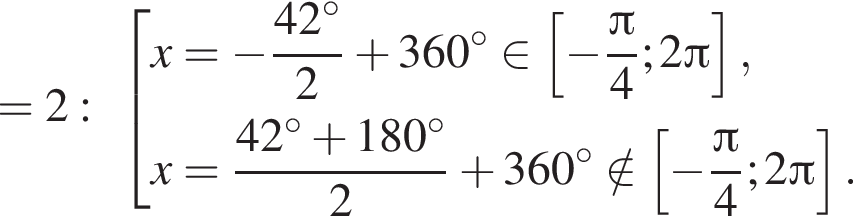
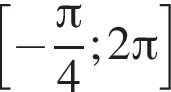 5 корней.
5 корней.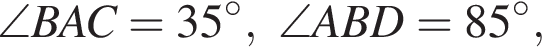 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...




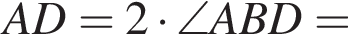
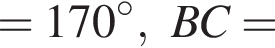
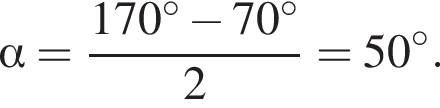
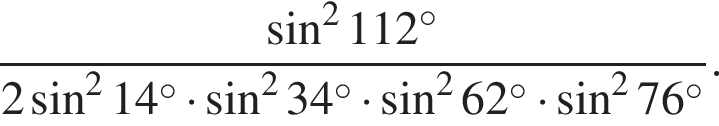

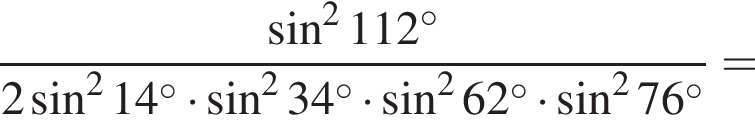
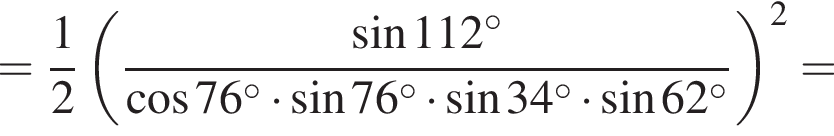
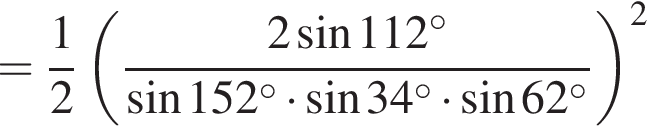
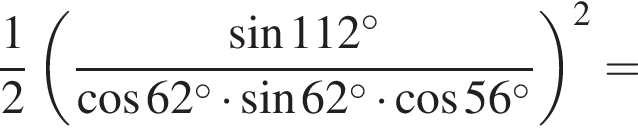
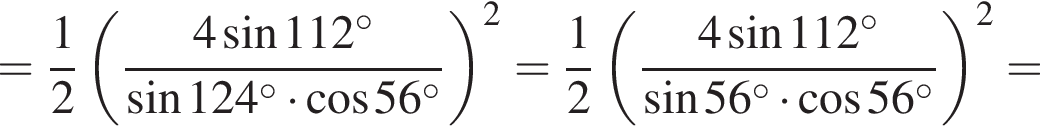
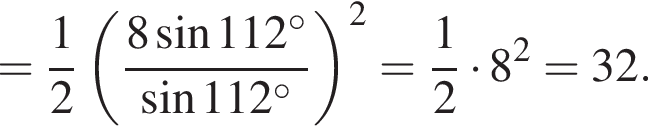
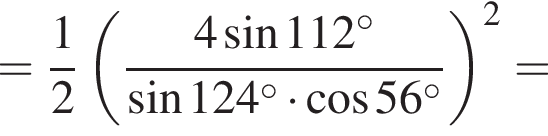
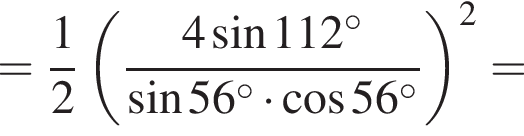
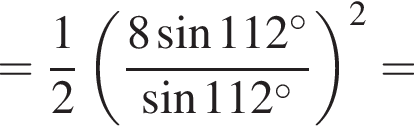
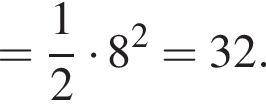
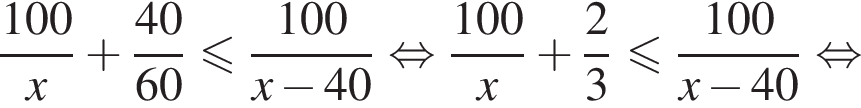
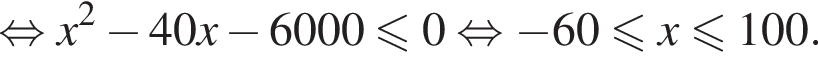
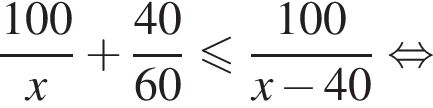
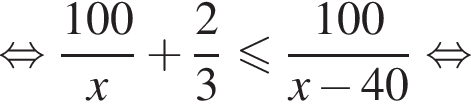
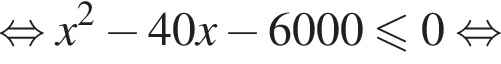

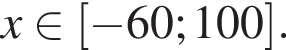 Таким образом, наибольшее значение скорости первого автомобиля — 100 км/ч.
Таким образом, наибольшее значение скорости первого автомобиля — 100 км/ч.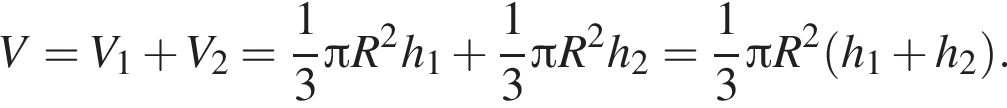
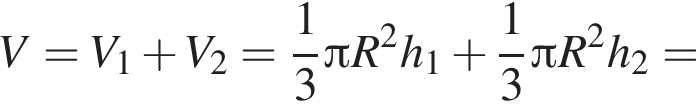
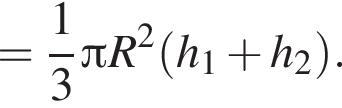
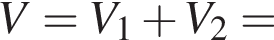
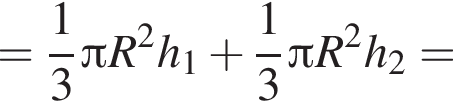
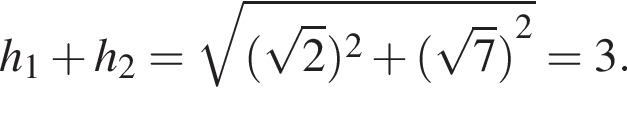
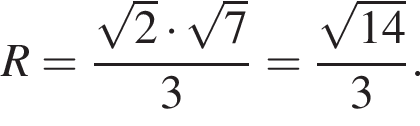
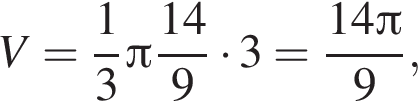 откуда
откуда 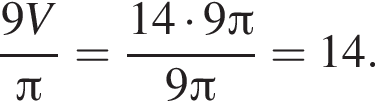
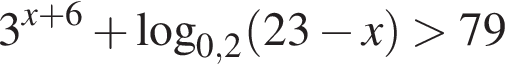 равно ...
равно ...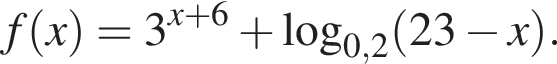 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 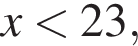 и что на
и что на 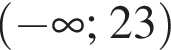
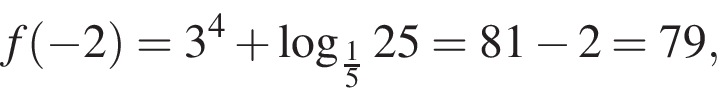 неравенство верно для всех x из
неравенство верно для всех x из 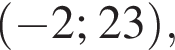 который содержит 24 целых числа.
который содержит 24 целых числа.